要计算两条曲线之间趋势的相似程度，具体来说：

对于两个函数（输出是一维的，输入不一定），如果在各个区间上的单调性排列相同，则认为是趋势相似的，例如 y=x^2 和 y=3x^2 就是相似的，而 y=x^2 和 y=-x^2 是不相似的

这里要求能判断变化快慢不同和截距不同的函数是相似的，对相位不同不做要求

DTW#

Dynamic Time Warping，动态时间规整

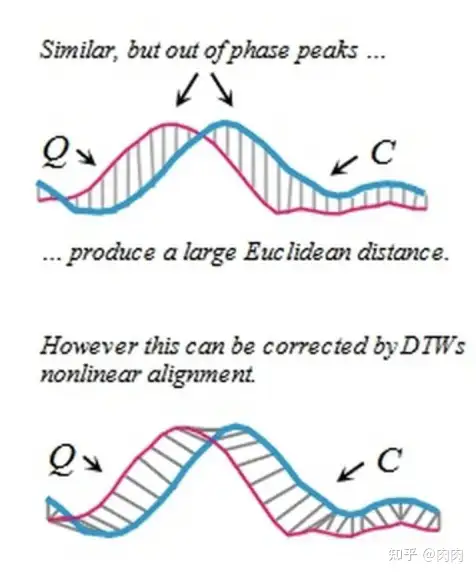
DTW 可以计算两个时间序列的相似度，尤其适用于不同长度、不同节奏的时间序列（比如不同的人读同一个词的音频序列）。 DTW 将两个序列拉伸放缩，使得两个序列的形态尽可能的一致，得到最大可能的相似度。

实现上，DTW 是用动态规划计算一个「最短路径问题」：

有矩阵 Dnm（n 是序列 A 的长度，m 是序列 B 的长度），Dij 是 Ai 和 Bj 的距离，现在从左上角 D11 开始，要到达右下角 Dnm，每次只能往右/下/右下方向前进。求最短路径？

表现在图像，最后 DTW 会尽可能把相似的点联系起来，这是欧氏距离无法直接做到的。

实现算法如下：

def dtw_similarity(s1, s2):

    def ed(m, n):
        return np.sqrt(np.sum((m - n) ** 2))

    a = s1 / np.linalg.norm(s1)
    b = s2 / np.linalg.norm(s2)
    D = np.zeros((len(a)+1, len(b)+1))
    D[1:, 1:] = ed(a, b)
    for i in range(1, len(a)+1):
        for j in range(1, len(b)+1):
            D[i][j] += min(D[i-1, j], D[i, j-1], D[i-1, j-1])
    return D[-1][-1]

这里的代码只实现了两个序列之间的比较，也就是默认输入是一维的。

样条插值法#

这种方法的思路就是先假定输入的函数符合某种分布，然后用分布去拟合得到特征系数，将「曲线趋势的相似度」转换为「特征系数的相似度」，后者是向量，可以用余弦相似度之类的方法实现。

多项式拟合#

from scipy.optimize import curve_fit

def curve_similarity(x, y1, y2):  
    # 定义模型函数
    def f(x, a, b, c, d, e):
        return a * x**4 + b * x**3 + c * x**2 + d * x + e

    def cosine_similarity(a,b):
        return np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b))

    params1, cov1 = curve_fit(f, x, y1)
    params2, cov2 = curve_fit(f, x, y2)
    return cosine_similarity(params1, params2)

广义加性模型拟合#

import pygam

def gam_similarity(x, y1, y2):

    def cosine_similarity(a,b):
        return np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b))

    model = pygam.LinearGAM(n_splines=10) #样条参数为 10
    
    model.fit(x, y1)
    params1 = []
    for i,term in enumerate(model.terms):  
        if term.isintercept:
            continue
        params1.extend(model.partial_dependence(term=i))
    
    model.fit(x, y2)
    params2 = []
    for i,term in enumerate(model.terms):
        if term.isintercept:
            continue
        params2.extend(model.partial_dependence(term=i))
    return cosine_similarity(params1, params2)