遗传算法是智能优化算法、随机自适应的全局搜索算法。启发于进化论、遗传学说

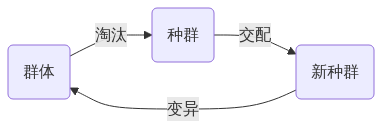
生物进化过程#

「群体」淘汰部分「个体」，选择剩下的个体作为「种群」
「种群」的个体交配产生「新种群」
「新种群」部分个体变异产生「群体」

算法与过程对应#

群体 - 一组问题搜索空间
种群 - 选择后的新群体
染色体 - 问题有效解编码串
基因 - 问题解的一个编码单元
适应能力 - 染色体的适应值
交配 - 染色体交换部分基因得到新染色体
变异 - 染色体某些基因数值变化
进化结束 - 算法满足终止条件

算法过程：

1. 随机生成一组个体
2. 根据适应度评估个体
3. 使用遗传操作进行演化：选择 交叉 变异
4. 重新评价适应值，更新最优个体

应用（优化问题）#

$\min 4x^3+3x^2-6x+1, x \in [-1,1]$ 求解精度为小数点后两位

编码并设计适应度 F(x)#

-1, 1 精度 2 位 -> 200 等分
-> 8 位二进制编码串 y 表示（染色体y）
-> x 与 y一一对应（个体x）
-> f(x) -> F(x)

round((upper- lower)10^t)<=2^L-1

二进制y -> x=lower+y*(upper-lower)/(2^L-1)

适应度函数：F(x)=1/(1+f(x))

算法过程#

设种群规模 N=50，random 产生 50 个染色体，选最大的 F(x) 对应 y

选择：轮盘赌法选择最适应的个体进行繁殖
交叉：两个个体染色体交配
变异：随机改变个体基因

轮盘赌法：p(i) 为 i 被选择的概率 $p(i)=\frac{F(x_i)}{\sum F(x)}$ （F(x)归一化）

num_items = 8 # 染色体位数
pop_size = 50 # 种群数量
num_iter = 100 # 迭代次数
selection_rate = 0.5 
mutation_rate = 0.01

def init_population():
  population = []
  for i in range(pop_size):
      chromosome = []
      # 初始化染色体
      for j in range(num_items):
          chromosome.append(random.randint(0,1)) 
      # 加入种群
      population.append(chromosome) 
  return population

def fitness(chromosome):
  x = -1 + int(chromosome, 2) * 2/(2^8-1)
  f = 4*x**3+3*x**2-6*x+1
  return 1 / (1 + f)

def selection(population): 
  population_fitness = [fitness(chromosome) for chromosome in population]
  # 根据适应度降序排序的population数组
  sorted_population = [x for _,x in sorted(zip(population_fitness, population), reverse=True)] 
  # 返回前selection_rate占比的population
  return sorted_population[:int(selection_rate * len(population))]

def crossover(parent1, parent2):
  crossover_point = random.randint(0, num_items-1)
  child1 = parent1[:crossover_point]+parent2[crossover_point:]
  child2 = parent1[crossover_point:]+parent2[:crossover_point]
  return child1, child2

def mutation(chromosome):
  for i in range(num_items):
      if random.random() < mutation_rate:
          j = random.randint(0, num_items-1)
          chromosome[i], chromosome[j] = chromosome[j], chromosome[i]
  return chromosome

def gengtic_algorithm():
  population = init_population()
  for i in range(num_iter):
      selected_population = selection(population)
      offspring_population = []
      for j in range(pop_size - len(selected_population)):
          [parent1, parent2] = [ random.choice(selected_population) for _ in range(2)]
          child1, child2 = crossover(parent1, parent2)
          [child1, child2] = [mutation(item) for item in [child1, child2]]
          offspring_population += [child1, child2]
      population = selected_population + offspring_population
      print("best: ", max(population, key=fitness), fitness(max(population, key=fitness)))